Exercise 5: Multi-Dimensional Arrays
Prerequisite
You have completed Exercise 4.
Learning Outcomes
Be comfortable writing simple C programs that involve 2D arrays.
Deadline
This exercise is part of the CS1010 formative assessment. Submit your solution before 21 October 2024, 23:59 to receive feedback and earn your achievement badges.
Acceptance Link
The link to accept the exercise is not available publicly. Visit Canvas for the link.
Concepts and Difficulty
| Question | Fixed 2D Arrays | Dynamic 2D Array | Jagged Array | Difficulty | |
|---|---|---|---|---|---|
| 1 | Add^ | ||||
| 2 | Echo | ||||
| 3 | Line^ | ||||
| 4 | Popular^ | ||||
| 5 | Contact | ||||
| 6 | Social |
^: Questions 2, 3, and 4 may serve as in-class exercises during the lab session in Week 9.
CS1010 I/O Library
You may need to use a new collection of functions available in the CS1010 I/O library for this exercise onwards.
cs1010_read_word_arraycs1010_read_line_array
Question 1: Add
Write a program add that reads two 3x3 matrices of integers \(M\) and \(N\) from the standard inputs and prints the resulting matrix \(M + N\) to the standard output.
For example,
\(\begin{pmatrix} 3 & 1 & 2\\ 0 & 4 & 1\\ 3 & 5 & 0 \\ \end{pmatrix}\) + \(\begin{pmatrix} 1 & -1 & 3\\ -1 & 2 & 0\\ 0 & 1 & 3 \\ \end{pmatrix}\) = \(\begin{pmatrix} 4 & 0 & 5\\ -1 & 6 & 1\\ 3 & 6 & 3 \\ \end{pmatrix}\)
If the two input matrices are
1 2 3 | |
and
1 2 3 | |
then print to the standard output
1 2 3 | |
Sample Run
1 2 3 4 5 6 7 8 9 10 | |
Question 2: Echo
Write a program echo that reads a 2D matrix of integers and prints the matrix back to the standard output.
The input consists of the following:
- the first two numbers correspond to \(R\), the number of rows, and \(C\), the number of columns of the matrix respectively
- the next line contains \(R\) x \(C\) integers.
Print to the standard output:
- \(R\) rows of numbers, each row contains \(C\) integers, corresponding to the rows of the matrix.
Your code should contain two functions:
1 2 3 | |
to allocate, read, and return the matrix (return NULL if allocation fails).
and
1 2 3 | |
to print the matrix.
Sample Run
1 2 3 4 5 6 | |
Question 3: Line
Write a program that draws a white line on an image with a black background of sizes \(W\) and \(H\).
The line is specified as two coordinates (\(x_1\), \(y_1\)) and (\(x_2\), \(y_2\)). The top left corner has a coordinate (0,0). The x coordinates increase to the right; the y coordinates increase to the bottom.
Let (\(x\), \(y\)) be any point that lies on this line, then we have:
We can rearrange and get:
Let
be the slope of the line.
If the line passes through (\(x\), \(y\)), then it passes through (\(x + 1\), \(y + m\)).
Mathematically, x and y are floating-point numbers. But, when we draw the line in an image, we have to round them into integers. This process is called rasterization in computer graphics.
To draw a rasterized straight line, we can then loop through different values of \(x\), from \(x_1\) to \(x_2\), and update the corresponding value of \(y\) (by repeatedly adding \(m\) every time \(x\) increments by 1).
Since \(y\) is a floating-point number, we round \(y\) to the nearest integer and draw the line at pixel (\(x, y\)). You may find the function round from math.h useful.
We will draw the output in an image format called PGM. Each pixel of the image has a value ranging between 0 and 255. For this question, we draw images with two colors: 0 for the black background and 255 for the white line.
Your program should read from the standard input:
- Two positive integers, \(W\) and \(H\) (\(W\) > 1, \(H\) > 1)
- Four non-negative integers, \(x_1\), \(y_1\), \(x_2\), \(y_2\), that corresponds to the two endpoints (\(x_1\), \(y_1\)) and (\(x_2\), \(y_2\)) of the line. The slope of the line is guaranteed to be between -1 and 1. Furthermore, \(x_2\) > \(x_1\).
Your program should print to the standard output,
-
The first line contains the string "P2"
-
The second line contains two integers, the width \(W\) and height \(H\) of the image
-
The third line contains the number 255
-
The rest of the output contains \(W\times H\) integers, each having a value of either 0 or 255. Each value corresponds to a pixel in the output image. The order of the pixels is from left to right, top to bottom. Each row of the image must be printed on a separate line.
If you pipe your output into ~cs1010/bin/viu, you can visualize your output as an image.
1 | |
Note that if your image to too big to fit your terminal, viu will resize your image.
The output for this question must match exactly the expected output, including new lines and spaces. Since white spaces are not visible, you can use pipe the output through a Unix tool called sed (similar to onigiri in Exercise 2) to replace spaces with dots:
1 | |
Sample Runs
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 | |
Question 4: Popular
We can measure the popularity of a person by how many friends a person has. We assume that "friend" is a symmetric relation. If A is a friend of B, then B is a friend of A. Because of this, we can represent friendships between people as a lower triangular matrix (using a jagged 2D array). A proper type to store in each element of the matrix is bool. To simplify our life, however, we store each element of the matrix as a char, with '1' representing a friendship connection, and '0' otherwise. The friendship for \(n\) people is thus an array of \(n\) strings, each string containing characters of '0' and '1' only. The first row of the matrix is a string of length one; the second row is of length two; the third row, length three, etc. The last character of each string (i.e., the diagonal of the matrix) is 1 as we assume everyone is a friend with him/herself.
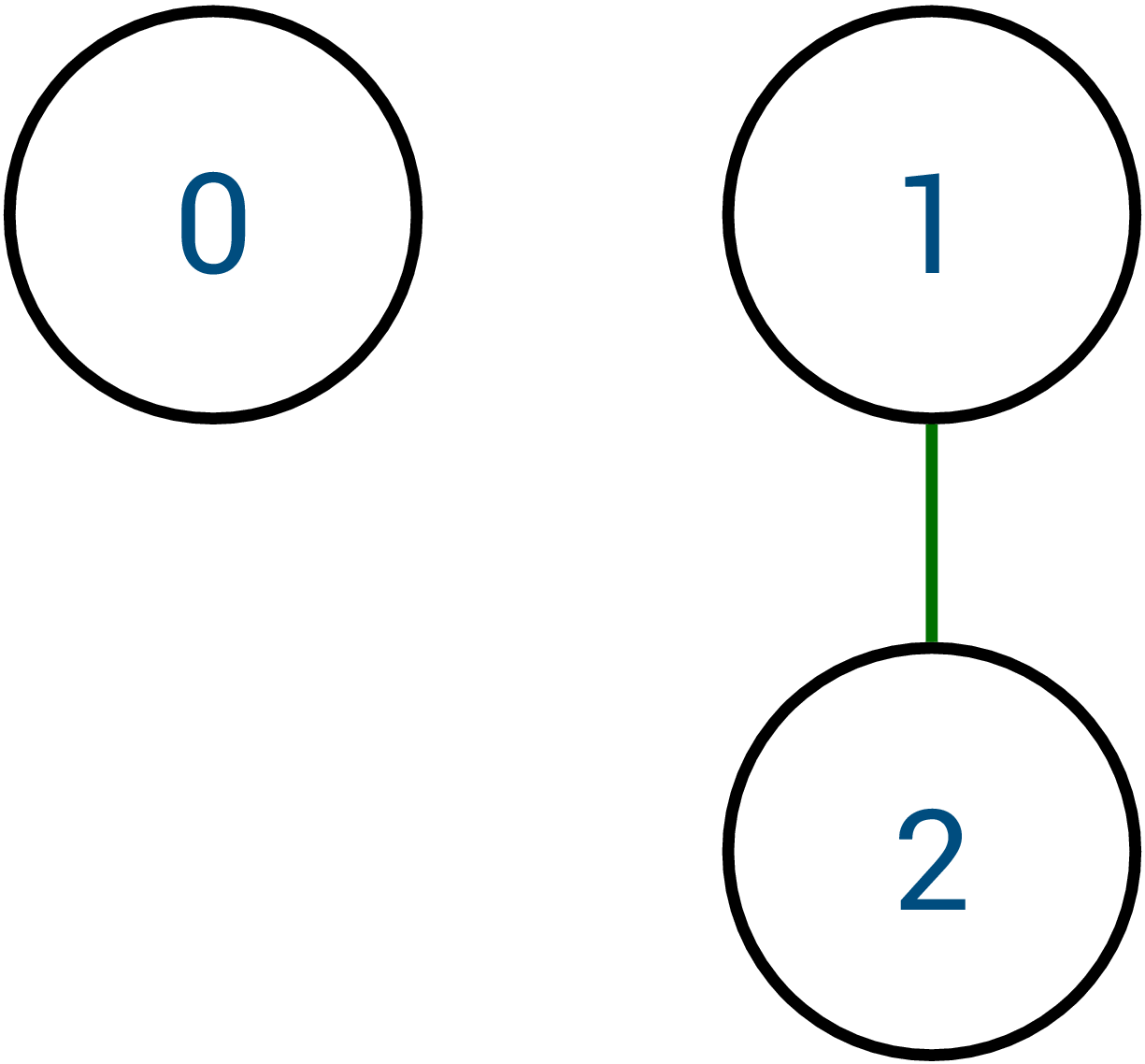
For instance, suppose we have the following friendship relations. We represent each person with id 0, 1, 2, ... Person with id \(i\) has its information stored in Row \(i\) and Column \(i\). Recall that if Row \(i\) and Column \(j\) is 1, it means that Person \(i\) is a friend of Person \(j\).
1 2 3 | |
The relation indicates that Person 1 and 2 are friends with each other. Person 0 is not a friend of 1 and 2.
The example below adds another person, Person 3, who is a friend of Person 0 and Person 2.
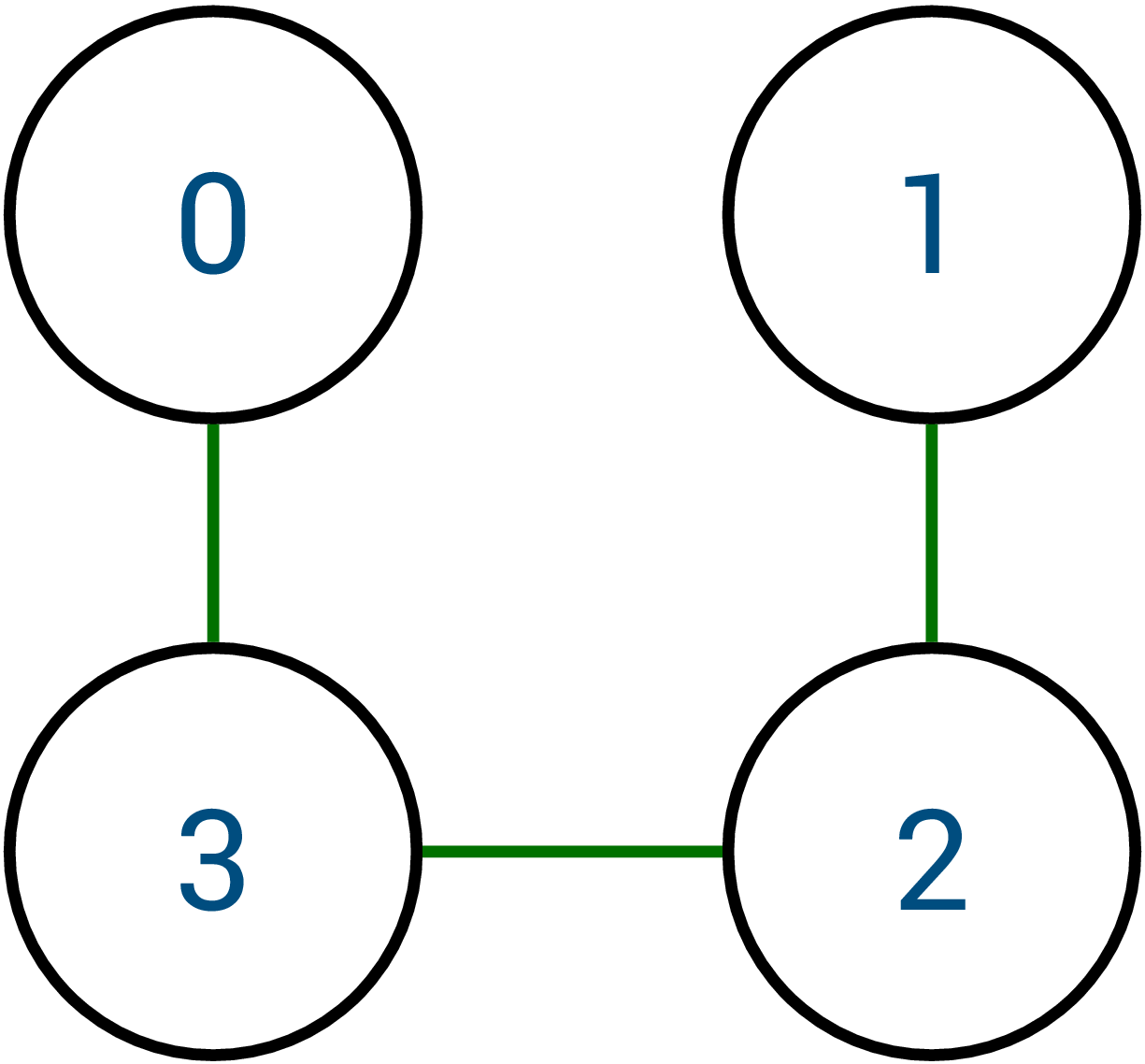
1 2 3 4 | |
Write a program popular, that reads from standard input:
- a positive integer \(n\),
- followed by \(n\) lines of strings consisting of '1' or '0' representing the friendship among these \(n\) people.
Print, to the standard output,
- the id of the person who is the most popular (i.e., with the most number of friends). We break ties by preferring the person with a smaller id.
- the number of friends that the person has.
The purpose of this question is for you to practice using a jagged 2D array. Hence, you are not allowed to store the input matrix or intermediate matrices using a rectangular array, or you risk being penalized heavily for this question.
Sample Runs
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 | |
Question 5: Contact
Contact tracing is an important step to contain a pandemic. Suppose we are given the information on who is in contact with whom. We wish to answer the following questions:
- Given two people A and B, have they been directly in contact with each other?
- Given two people A and B, is there a common person that they have been in contact with? In other words, is there a third person C, where (i) A and C have been in contact with each other, and (ii) B and C have been in contact with each other?
We assume that "contact" is a symmetric relation. If A has been in contact with B, then B has been in contact with A too. Because of this, we can represent the contact traces between n people as a lower triangular matrix (using a jagged 2D array). Similar to Question 4, we store each element of the matrix as a char, with '1' representing a contact, and '0' otherwise. The contact traces for \(n\) people is again an array of \(n\) strings, each string containing characters of '0' and '1' only. The first row of the matrix is a string of length one; the second row is of length two; the third row, length three, etc. The last character of each string (i.e., the diagonal of the matrix) is 1 since everyone has contact with him/herself.
Write a program contact, that reads from standard input:
- a positive integer \(n\),
- followed by \(n\) lines of strings consisting of '1' or '0' representing the contact traces of these \(n\) people.
- followed by two positive integers \(j\) and \(k\), representing the ids of a pair of people we are interested in querying. An input of \(i\) corresponds to the person whose contact information is stored in Row \(i\) and Column \(i\).
Print, to the standard output, the following information:
- "direct contact" if there is direct contact between \(j\) and \(k\)
- "contact through x" if there is no direct contact but there is an indirect contact between \(j\) and \(k\) through a third person \(x\) (replace \(x\) with the actual id). If there are multiple such people, output the person with the smallest id.
- "no contact" if there is no direct or indirect contact through a third person in the contact traces.
The purpose of this question is for you to practice using a jagged 2D array. Hence, you are not allowed to store the input matrix or intermediate matrices using a rectangular array, or you risk being penalized heavily for this question.
Sample Runs
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 | |
Question 6: Social
You should solve this question after solving Questions 4 and 5. The functions you wrote for Questions 4 and 5 might be useful for solving this question.
In this question, we are interested in understanding the social network of a group of people. Suppose that person A is a friend of person B, then we say that A is connected to B with one hop, or A is one hop away from B.
Consider a friend of B, say C, who is not a friend of A. So C is a friend of a friend of A. We say that C is two hops away from A, and there is a chain of friendship of 2 hops between A and C (A -> B -> C).
Suppose there are \(n\) people, and we know the social network of these \(n\) people -- i.e., we know who is a friend with whom. We call the network a social network of degree 1. Your task is to compute a social network of degree \(k\), representing who is connected to whom via a friendship chain of up to \(k\) hops.
Similar to Question 4, we assume that friendship is bi-directional -- if A is a friend of B, then B is a friend of A. We represent a social network as a lower triangular matrix (using a jagged 2D array) in the same format as Question 4, where a 1 in Row \(i\) and Column \(j\) means Person \(i\) and Person \(j\) are friends; 0 otherwise.
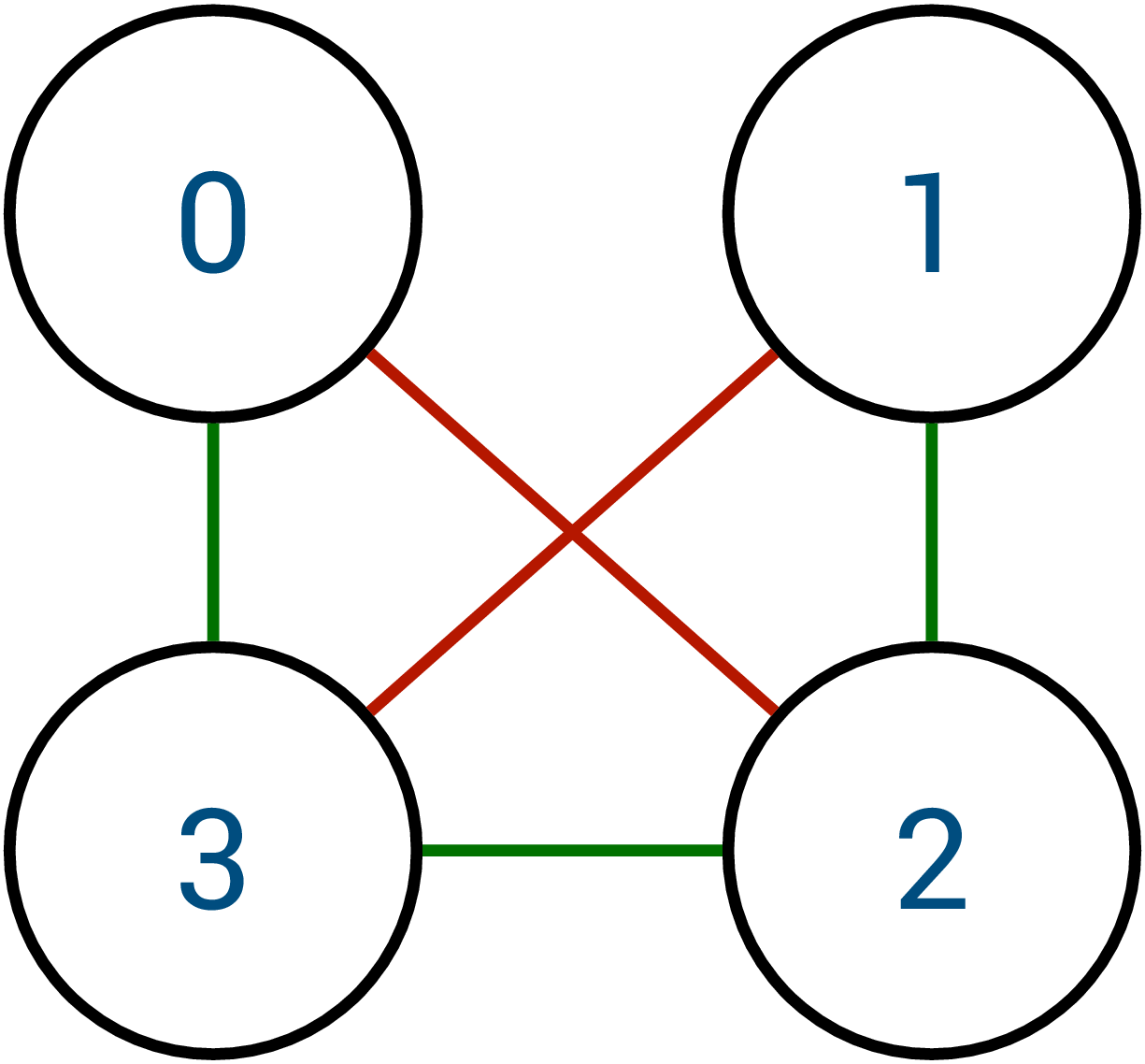
The social network below shows the friendship relations between four people: Person 0 is friends with Person 3, Person 1 is friends with Person 2, and Person 2 is friends with Person 3.

1 2 3 4 | |
Suppose now we consider the social network of degree 2. Person 0 is two hops away from Person 2 (Person 0 knows Person 3, and Person 3 knows Person 2). Person 1 is also two hops away from Person 3 (Person 1 knows Person 2 and Person 2 knows Person 3).
The social network of degree 2 becomes:
1 2 3 4 | |
The new 2-hop friendship is shown in red:
Consider another example (Test Case 8). Person 2 are friends of 0 and 1. Person 3 and Person 1 are friends; Person 4 and Person 0 are friends.
1 2 3 4 5 | |

The social network of degree 2 becomes
1 2 3 4 5 | |
The new 2-hop friendship is shown in red:

There are additional 2-hop connections in the network between Person 2 and Person 4 (through common friend Person 0); Person 0 and Person 1 (through common friend Person 2); and Person 2 and Person 3 (through common friend Person 1).
The social network of degree 3 becomes
1 2 3 4 5 | |
The new 3-hop friendships are shown in blue:
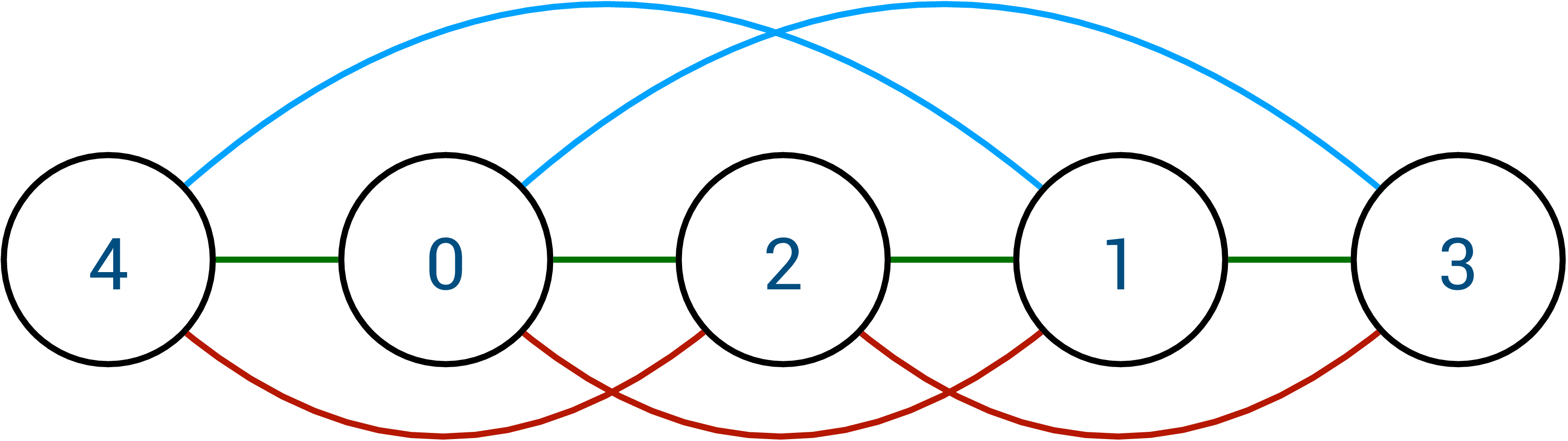
Person 1 and Person 4 are three-hop friends through either Person 0 or Person 2. Person 0 and Person 3 are also three-hop friends through Person 1 or Person 2. Note that Person 3 and Person 4 are NOT 3-hop friends. They are 4-hop friends through Person 2.
Write a program social, that reads from standard input two positive integers \(n\) and \(k\), followed by \(n\) lines of strings consisting of '1' or '0' representing the social network of degree 1 of these \(n\) people. Print, to the standard output, the social network of degree \(k\) formed by friendship chains of up to \(k\) hops.
Hint
There are many ways to solve this problem. The most straightforward way is to compute the social network formed by a friendship chain of degree \(i\), \(N(i)\), changing \(i\) from 1 to \(k\).
- \(N(1)\) is just the input;
- \(N(2)\) can be computed in a similar way to how you solved Question 2.
- Now, given \(N(i-1)\) and \(N(1)\), can you compute \(N(i)\)?
Sample Runs
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 | |