Exercise 5: Square, Escape, MagicSquare

This is a programming exercise for you to solve on your own. You can submit but it will not be graded. Test cases are provided for the exercises so that you can test and check on your own if your code is correct. Feel free to discuss your solution with your peers or your TAs.

Prerequisite

• You are able to access the CS1010 programming environment.
• You are familiar with basic UNIX CLI and using terminal-based editor vim.
• You have a GitHub account and have setup .gitconfig (see Exercise 1).

Learning Outcomes

• Be comfortable writing correct C programs that involve if, else, loops, logical statements, memory management, and arrays.
• Be able to decompose a more complex problem into smaller subproblems and write functions to solve the sub-problems.
• Be able to use nD arrays to solve problems

Setup

• Click on this link to accept the exercise.
• Log in to one of the hosts of CS1010 programming environment (PE)
• Run the following on the command line on one of the PE hosts:

~cs1010/get-ex05

• You should see a new subdirectory ex05-<githubid> in your current working directory, where githubid is your GitHub ID.
• Inside that directory, you should see a bunch of files:
  • square.c, escape.c, and magicsquare.c are the most important files. They are the C code that you should edit to solve the exercise.
  • inputs and outputs are subdirectories that contain test inputs and test outputs. We use the same convention as Exercise 1 so you should be familiar with them.
  • Makefile: This is the configuration for the tool make that we use to automate the compilation and testing of the programs.
  • test.sh: This is a bash script for testing your code.

Solving The Assignments

• Edit the .c files on the PE hosts to solve the corresponding question as described below.
• You can assume that all test inputs are valid inputs.
• To compile and run the given tests with the sample inputs and outputs, run on the command line,

make

This will compile all your C files and if there is no error, run the test scripts.

Submission

When you are ready, run the following command while you are in the exercise directory:

~cs1010/submit-ex05

The .c files will be uploaded to GitHub. You can submit multiple times. As an exercise is not graded, submitting your code only serves the purpose of archiving your work for backup purposes.

---

Question 1: Square

Recall Question 5 from PE1, where you are asked to draw patterns of squares using recursion. In this problem, you are to solve the same problem using loops and arrays, instead of recursion.

Write a program square that reads, from the standard input, an integer $n$ and prints, to the standard output, a set of squares with width $n$, $n - 4$, $n - 8$, .. until we reach either the width of 3, 2, 1, or 0. The smaller square is contained in the larger squares. The squares do not touch each other. A square has exactly one space between itself and the next larger square (if exists), in each direction.

Here is how we can use loops and a 2D array to solve this problem. Suppose we have a 2D char array of size $n \times $n. We can "draw" in this array by filling it with ' ' or '#'. We can then print this array to the standard output to display the pattern on the screen.

Write a program square, that reads from standard inputs, an integer n, and prints to standard output the expected pattern of squares.

Sample Run 1

ooiwt@pe119:~ex05-weitsang$ ./square
1
#
ooiwt@pe119:~ex05-weitsang$ ./square
2
##
##
ooiwt@pe119:~ex05-weitsang$ ./square
3
###
# #
###
ooiwt@pe119:~ex05-weitsang$ ./square
4
####
#  #
#  #
####
ooiwt@pe119:~ex05-weitsang$ ./square
5
#####
#   #
# # #
#   #
#####
ooiwt@pe119:~ex05-weitsang$ ./square
6
######
#    #
# ## #
# ## #
#    #
######
ooiwt@pe119:~ex05-weitsang$ ./square
7
#######
#     #
# ### #
# # # #
# ### #
#     #
#######
ooiwt@pe119:~ex05-weitsang$ ./square
10
##########
#        #
# ###### #
# #    # #
# # ## # #
# # ## # #
# #    # #
# ###### #
#        #
##########

Question 2: Escape

Ackbar is lost in a maze that contains traps. You are his only hope! Send him instructions remotely to help him escape.

The maze is represented as a $m \times n$ grid of cells, where each cell can be of the following:

1. A wall, denoted by character '#'
2. An empty space, denoted by character '.'
3. A trap, denoted by character '*'

To help Ackbar, you give Ackbar a series of instructions denoted by U,D,L, or R. U instructs Ackbar to move to the cell one row above. D instructors Ackbar to go to the cell one row below. L instructs Ackbar to move to the cell one column to the left, and R instructs Ackbar to move to the cell one column to the right. Ackbar follows the instructions in the order they are given, and it only moves one cell adjacent by following each instruction, with the following exceptions:

1. If an instruction leads Ackbar to a wall, Ackbar's path is blocked and he stays in position. He continues with the next instruction if there is one.

2. if an instruction leads Ackbar to a trap, he is trapped and is unable to move anymore. All subsequent instructions have no effect on Ackbar. Poor Ackbar!

3. If the instruction leads Ackbar to anywhere outside the maze, Ackbar escapes happily and any instruction after that is ignored.

For convenience, we index the row as 0 to $m$-1 from top to bottom, and column as 0 to $n$-1 from left to right.

Write a program escape, that reads (from the standard input) two positive integers $m$ and $n$, followed by $m$ rows with $n$ characters in each row. These characters denote the maze of size $m \times n$. Each character can only be #, ., * or A, where A denotes the initial position of Ackbar on an empty space. It is guaranteed only one A exists in the input. Your program then reads a string denoting the order you give to Ackbar. Each character can only be U, D, L, or R. Finally, your program prints, to the standard output, one of the following:

1. If Ackbar escaped from the maze after following some instructions, print "ESCAPED!"
2. If Ackbar is trapped due to your unwise instruction, print "IT'S A TRAP!"
3. If Ackbar is still stuck in the maze but not trapped after following all the instructions, print the position of Ackbar as x y where x and y denotes the row and column of Ackbar's position after following all your instructions.

Sample Run

ooiwt@pe119:~/ex05-weitsang$ ./escape
5 5
#.###
#...#
#.A##
#.*.#
#####
RLU
1 1
ooiwt@pe119:~/ex05-weitsang$ ./escape
5 5
#.###
#...#
#.A##
#.*.#
#####
RLUUU
ESCAPED!
ooiwt@pe119:~/ex05-weitsang$ ./escape
5 5
#.###
#...#
#.A##
#.*.#
#####
LURLUUUDLR
ESCAPED!
ooiwt@pe119:~/ex05-weitsang$ ./escape
5 5
#.###
#...#
#.A##
#.*.#
#####
UDDLUUUUU
IT'S A TRAP!

Question 3: Magic

A magic square is a grid of $n \times n$ with each cell filled with a distinct number from 1 to $n^2$, such that, the sum of each row, column, or diagonal are the same.

Write a program, magicsquare, that constructs a magic square of size $n \times n$, where $n$ is odd.

There are multiple ways we can construct such as magic square. For this question, you shall follow the following algorithm:

1. Put 1 at center column of the top row

2. Each of the remaining numbers is placed one row up and one column to the right of the previous number. This may not always work when we reach the edge of the square or when the cell one row up and one column to the right is occupied. In such a case, you should follow the rules below:

   • A. If a number's cell is already taken, put it one row below the position of the previous number;
   • B. If a number's cell is above the top row, stay in that column and put it in the bottom row;
   • C. If a number's cell is outside of the rightmost column, stay in that row and put it in the leftmost column;
   • D. If a number's cell is outside both the topmost row and the rightmost column put it one row below the previous number.

The following example shows how we fill up a $5\times 5$ magic square.

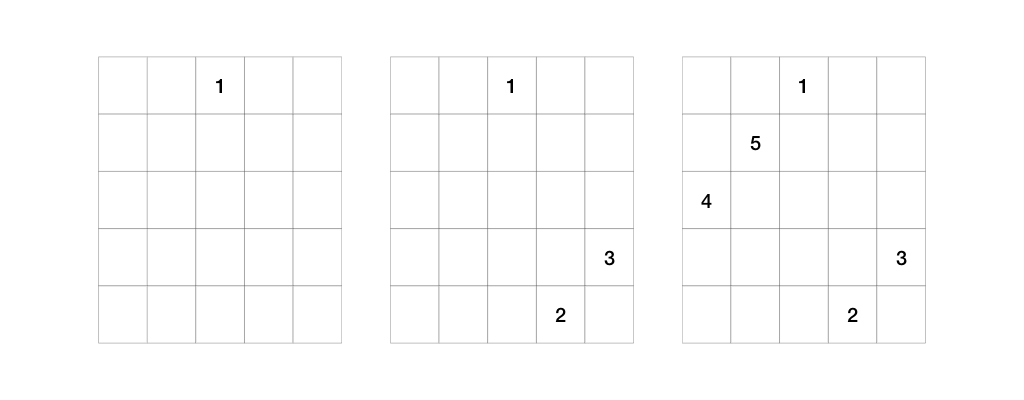
The number 2 is filled above the top row, so we apply Rule B. The number 4 is filled outside the rightmost column, so we apply Rule C.

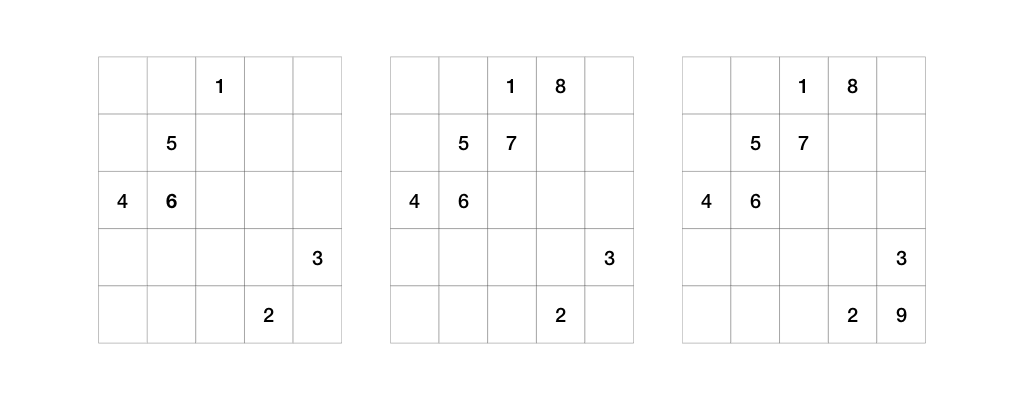
The cell for number 6 is already taken (by 1), so we apply Rule A.

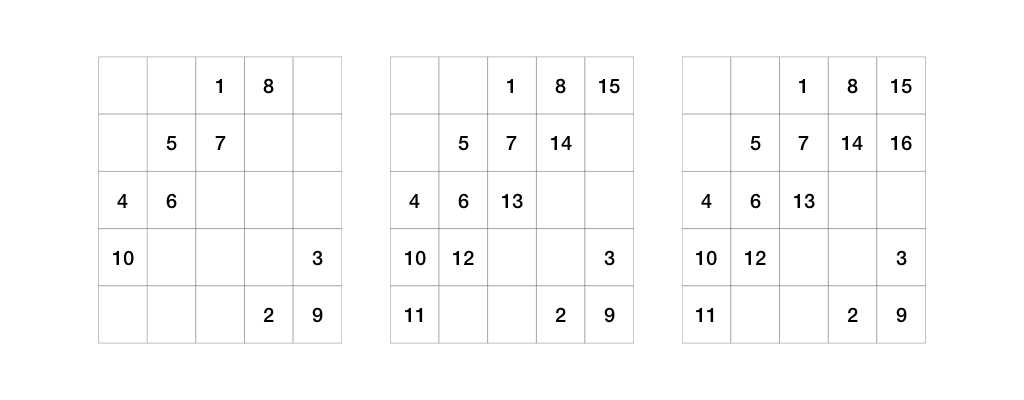
The number 16 goes outside both the topmost row and the rightmost column, so we apply Rule D.

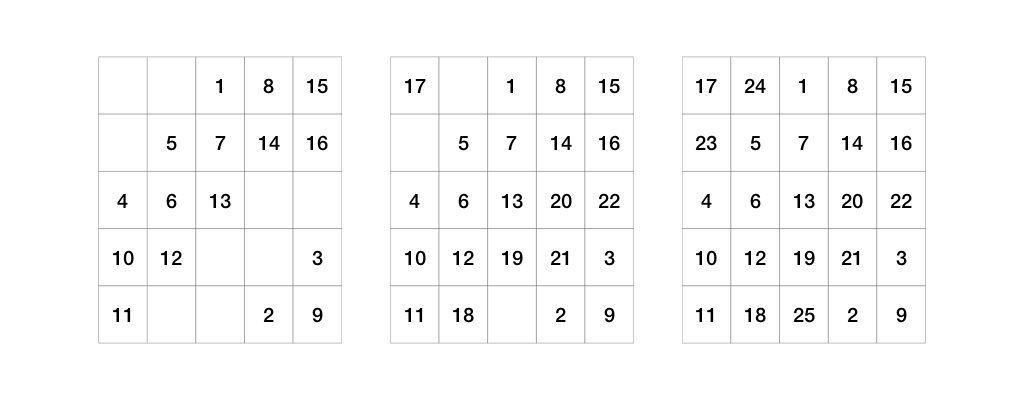
Write a program magicsquare, that reads (from the standard input) an odd integer $n$ and prints (to the standard output) $n$ rows with $n$ numbers in each row, denoting the constructed magic square using above described method.

Sample Run

ooiwt@pe119:~/ex05-weitsang$ ./magicsquare
3
8 1 6
3 5 7
4 9 2
ooiwt@pe119:~/ex05-weitsang$ ./magicsquare
7
30 39 48 1 10 19 28
38 47 7 9 18 27 29
46 6 8 17 26 35 37
5 14 16 25 34 36 45
13 15 24 33 42 44 4
21 23 32 41 43 3 12
22 31 40 49 2 11 20