PE2: Comments and Answer Keys

transpose

This is suppose to be a give-away question. We want to see if you can manipulate 2D arrays, including stepping through the elements, and allocating/deallocating the memory for them.

First, let's write some functions to allocate, read, print, transpose and free a matrix.

/**
 * Allocated and read a matrix from the standard input.  
 * The caller is responsible to free the matrix.  
 *
 * @param[in] row The number of rows to read.
 * @param[in] col The number of columns to read.
 * @return    A 2D array containing the matrix.
 */
double** read_matrix(long row, long col) 
{
  double **m = calloc(row, sizeof(double *));
  for (long i = 0; i < row; i += 1) {
    m[i] = cs1010_read_double_array(col);
    assert(m[i] != NULL);
  }
  return m;
}

/**
 * Allocated a 2D matrix of 0s.
 * The caller is responsible to free the matrix.  
 *
 * @param[in] row The number of rows to allocate.
 * @param[in] col The number of columns to allocate.
 * @return    A 2D array containing the matrix.
 */
double** alloc_matrix(long row, long col) 
{
  double **m = calloc(row, sizeof(double *));
  for (long i = 0; i < row; i += 1) {
    m[i] = calloc(col, sizeof(double));
  }
  return m;
}

/**
 * Print a given 2D matrix.
 *
 * @param[in] m   The matrix to print.
 * @param[in] row The number of rows to print.
 * @param[in] col The number of columns to print.
 */
void print_matrix(double **m, long row, long col) 
{
  for (long i = 0; i < row; i += 1) {
    for (long j = 0; j < col; j += 1) {
      cs1010_print_double(m[i][j]);
      if (j == col - 1) {
        cs1010_println_string("");
      } else {
        cs1010_print_string(" ");
      }
    }
  }
}

/**
 * Free the memory allocated for a 2D matrix.
 *
 * @param[in] m   The matrix to free.
 * @param[in] row The number of rows in the matrix m.
 */
void free_matrix(double **m, long row)
{
  for (long i = 0; i < row; i += 1) {
    free(m[i]);
  }
  free(m);
}

/**
 * Transpose a given matrix m1 and store the output in m2.
 *
 * @param[in]  m1  The given matrix to transpose.
 * @param[out] m2  The transposed matrix.
 * @param[in]  num_of_rows The number of rows in m1.
 * @param[in]  num_of_cols The number of rows in m2.
 */
void transpose(double **m1, double **m2, long num_of_rows, long num_of_cols) {
  for (long i = 0; i < num_of_rows; i += 1) {
    for (long j = 0; j < num_of_cols; j += 1) {
      assert(m1[i] != NULL);
      assert(m2[j] != NULL);
      m2[j][i] = m1[i][j];
    }
  }
}

The main program then looks like this:

int main() {
  long num_rows = cs1010_read_long();
  long num_cols = cs1010_read_long();

  double **m1 = read_matrix(num_rows, num_cols);
  double **m2 = alloc_matrix(num_cols, num_rows);

  transpose(m1, m2, num_rows, num_cols);

  print_matrix(m2, num_cols, num_rows);
  free_matrix(m1, num_rows);
  free_matrix(m2, num_cols);
}

palindrome

This is a classic programming question and is also fairly simple. We want to see if you knows how to manipulate a string. Here is a loop version:

bool is_palindrome(char *s) {
  long start = -1;
  long end = strlen(s);

  do {
    do {
      start += 1;
    } while (!isalpha(s[start]));

    do {
      end -= 1;
    } while (!isalpha(s[end]));

    if (tolower(s[start]) != tolower(s[end])) {
      return false;
    }
  } while (start < end);

  return true;
}

The two innwer loops skip the non-alphabetical characters at the beginning and at the end of the string. After we ensure that s[start] and s[end] are both alphabets, we compare the lower-case version. If they are different, then it is not a palindrome and we return false. Otherwise, we continue. If we have exhausted all the characters in the string and we have not returned false, then the string must be a palindrome.

Here is a recursive version:

bool is_palindrome(char *s, long start, long end) {
  if (start >= end) {
    return true;
  }

  if (!isalpha(s[start])) {
    return is_palindrome(s, start + 1, end);
  }

  if (!isalpha(s[end])) {
    return is_palindrome(s, start, end - 1);
  }

  if (tolower(s[start]) == tolower(s[end])) {
    return is_palindrome(s, start + 1, end - 1);
  }
  return false;
}

rotate

Getting 4 marks for this question is trivial (using a linear search). But trying to get all 9 marks is not so straight forward. It requires a tweak to the binary search to solve in $O(\log n)$ time. The fact that it requires $O(\log n)$ time hinted at the need to halve the array at every recursive call. To decide which half to search, we first have to analyze the properties of the input. The properties can be summarized as follows:

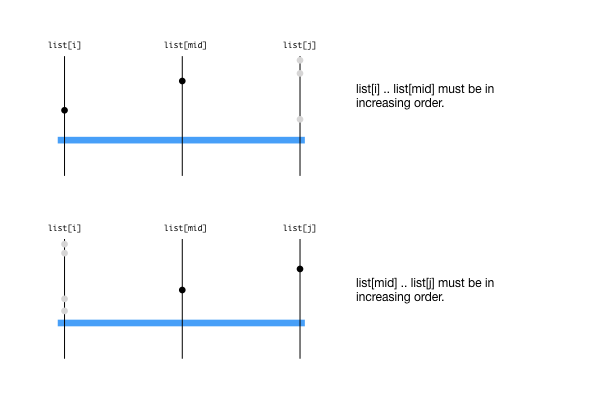
But once you have the cases above, the code is quiet straightforward. If q falls under the half that is a sorted array, then we perform binary search on that half, otherwise, we recursively call the function to search in the rotated and sorted array on the other half.

/**
 * Look for q in list[i]..list[j].
 *
 * @pre list is sorted.
 * @return -1 if not found, the position of q in list otherwise.
 */
long search(const long list[], long i, long j, long q) {
  if (j < i) {
    return -1;
  }

  long mid = (i+j)/2;
  if (list[mid] == q) {
    return mid;
  } 

  /*
   * - list[i]..list[mid] is strictly increasing.  So we do binary search
   *   if q falls within this range.  Otherwise, we recursively search 
   *   the other half (which is a rotated list).
   */
  if (list[i] < list[mid]) {
    if (list[i] <= q && q <= list[mid]) {
      return binary_search(list, i, mid-1, q);
    }
    return search(list, mid+1, j, q);
  }

  /*
   * - list[i]..list[mid] is rotated.  So we do a binary search on the 
   *   other half.
   */
  if (list[mid+1] <= q && q <= list[j]) {
    return binary_search(list, mid+1, j, q);
  }
  return search(list, i, mid-1, q);
}

Here, the function binary_search is the same one given in the lecture.

marcell

This question is designed to check if you know how to write efficient code. It is an extension to goldbach from PE1. The prerequisite to solving this question well is that you must know how to find a prime number in $O(\sqrt{n})$ time. If you have been paying attention to Assignment 2, PE1 Comments, and Unit 22, you should have what it takes to solve this.

Everyone's first instict would be to write a function is_prime and a function is_semiprime to check if a number is prime or semiprime. However, our second principle of writing efficient code avoid repetitive work, applies here. If you wrote these two functions, you will notice that we need to scan through numbers between 2 to $\sqrt{n}$ for an input $n$ for both functions. So we could combine them into one function:

long is_prime_or_semiprime(long n) {
  if (n <= 1) {
    return NEITHER;
  }
  for (long i = 2; i <= sqrt(n); i += 1) {
    if (n % i == 0) {
      if (is_prime(i) && is_prime(n/i)) {
        return SEMIPRIME;
      }
      return NEITHER;
    }
  }
  return PRIME;
}

Update: Line 6 of the function was originally:

      if (is_prime_or_semiprime(i) == PRIME && is_prime_or_semiprime(n/i) == PRIME) {

We have replaced the line with

      if (is_prime(i) && is_prime(n/i)) {

so that the running time can be analyzed to be $O(\sqrt{n})$ in a more straight forward manner.

With the above function, finding the number of pairs is not much different from goldbach:

  int counter = 0;

  for (long i = 2; i <= n/2; i += 1) {
    long p1 = is_prime_or_semiprime(i);
    if (p1 == PRIME || p1 == SEMIPRIME) {
      long j = n - i;
      int p2 = is_prime_or_semiprime(j);
      if ((p1 == PRIME && p2 == SEMIPRIME) || (p1 == SEMIPRIME && p2 == PRIME)) {
        counter += 1;
      }
    }
  }

bracket

This is meant to be the hardest question that separates A+ from A students. Note that, if we ignore condition 2(i) (a valid string can be a concatenation of two valid strings), a valid string is just a "palindrome" consisting of characters ({[<>]}), except that we match the opening brackets to the closing brackets instead of the same characters. If you solve that by modifying the recursive version of the palindrome code above, you should get some partial correctness marks.

The tricky part is to handle condition 2(i). So our recursive function has to tell us, if the input string contains a valid string, and where does it ends. One solution is to write a recursive function that "consumes" a valid string (and only a valid string) recursively, and returns the next character that is unconsumed. If the next character is \0, then the string must be a valid string, since everything is consumed.

Let's first write a couple of helper functions:

bool is_open(char c) {
  return c == '(' || c == '{' || c == '[' || c == '<';
}

The above checks if a given character is an open bracket.

bool is_matching_close(char c, char d) {
  return (c == '(' && d == ')') ||
    (c == '{' && d == '}') ||
    (c == '<' && d == '>') ||
    (c == '[' && d == ']');
}

The above checks if a pair of input characters are matching brackets.

And now, the recursive function to consume a valid string. It returns the index to the first character that is not consumed.

int consume_valid(char *string, int begin) {
  if (string[begin] == '\0') {
    return begin;
  }
  if (!is_open(string[begin])) {
    return begin;
  }

  int end = consume_valid(string, begin+1);
  if (is_matching_close(string[begin], string[end])) {
    return consume_valid(string, end + 1);
  }
  return begin;
}

Let's first look at Line 2-4. If the input string is empty, then by Rule 1 it is always valid.

Line 5-7 checks if the input string starts with a closing bracket. If so, it cannot be a valid string and the function consumes nothing. By Rule 2, it must starts with an open bracket. So we return begin since this is the index to the first unconsumed character.

When we reach Line 9, we can assert that the string begins with an open bracket. So we consume the string from index begin + 1 onwards recursively. By wishful thinking, we can assume that this function will consume a valid string and returns the index of the first unconsumed character.

We now check on Line 10, if this unconsumed character (string[end]) is a matching close bracket to string[begin], following Rule 2(ii). If it does not match, then we return begin (Line 13) since string[begin] is the first unmatched character (so the function spews out all the consumed characters and un-consumes them).

If Line 10 checks out, then the string from begin to end is valid, and we continue to recursively consume from character end + 1 onwards.

In main, we call the function as follows:

  int end = is_valid(str, 0);
  if (str[end] == '\0') {
    cs1010_println_string("yes");
  } else { 
    cs1010_println_string("no");
  }